Cours:TdFonctionsTableaux
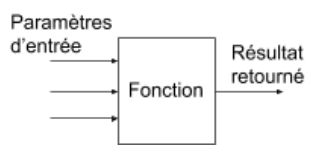
Rappel: Une fonction réalise un travail spécifique à partir de paramètres d’entrée: si le travail consiste en un calcul, le résultat du calcul est alors retourné.
Donc, pour pouvoir écrire une fonction:
- il faut déterminer ce dont la fonction a besoin pour effectuer sa tâche: ce sont les paramètres d’entrée.
- il faut alors écrire les lignes de code qui vont réaliser cette tâche,
- puis, si nécessaire, retourner le résultat.
Sommaire
Exercice 1
Ecrire les fonctions suivantes:
- une fonction qui calcule la valeur absolue d’un entier. Idem pour un flottant.
- une fonction qui calcule le minimum de deux entiers. Idem pour le maximum. Idem pour des flottants.
- une fonction qui calcule le module de l’impédance d’un condensateur C pour une certaine fréquence f. Idem pour une inductance L.
Exercice 2
Une fonction qui ne retourne aucun résultat est nommée procédure: le type retourné par la fonction est alors void.
Ecrire les fonctions (procédures) suivantes:
- une fonction (procédure) qui affiche tous les entiers compris entre zéro et n.
- une fonction (procédure) qui affiche tous les entiers pairs compris entre zéro et n.
- Ecrire une autre fonction pour les entiers impairs
- Pour les plus avancés: combiner ces deux fonctions en une seule, qui soit capable d’afficher les n premiers entiers pairs ou impairs à la demande.
- une fonction (procédure) qui affiche un entier n répété nb fois. Par exemple, si n=123 et nb=5, on obtient sur l’écran: 123 123 123 123 123.
Exercice 3
Ecrire une fonction qui calcule la factorielle d’un entier n.
Proposer une version itérative (avec une boucle) puis une version récursive.
Exercice 4
Statistiques
- Écrire une fonction qui calcule la moyenne des valeurs d’un tableau.
- Écrire une fonction qui calcule le minimum des valeurs d’un tableau.
- Écrire une fonction qui calcule l’écart-type des valeurs d’un tableau.
- Pour les plus avancés: Ecrire une fonction qui retourne une structure contenant la moyenne, l’écart-type et les extrema des valeurs d’un tableau.
Exercice 5
Mise à l’échelle (homothétie)
Écrire une fonction qui effectue une mise à l’échelle des valeurs d’un tableau:
- au départ, les valeurs du tableau sont comprises entre une valeur minimale et une valeur maximale
- après transformation, le tableau contient des valeurs comprises entre deux valeurs A et B spécifiées par l’utilisateur.
- Bien sûr, la disposition des points les uns par rapport aux autres n’est pas modifiée.
Exercice 6
Filtrage moyenne (type passe-bas)
Écrire une fonction qui modifie chacune des cases d’un tableau de la manière suivante:
- la valeur rangée en position i est remplacée par la moyenne des 3 valeurs rangées en case i-1, i et i+1.
- Bien sûr, la première et la dernière valeur du tableau ne sont pas traitées.
Exercice 7
Racine carrée
Ecrire une fonction qui calcule une valeur approchée de la racine carrée d'un nombre a avec une précision eps en utilisant la suite suivante:
un+1 = 1/2 (un + a * un )
Cette suite a pour propriété intéressante de converger rapidement vers la racine carrée de a, quelque soit le premier élément de la suite.
Pour les plus avancés: étendre ce calcul à la racine n-ième d’un nombre (cf https://fr.wikipedia.org/wiki/Méthode_de_Héron )
Exercice 8
Calcul de π
Calculer une valeur approchée de π de la manière suivante:
- tirer deux valeurs aléatoires comprises entre 0 et 1 en utilisant la fonction rand() et les ranger dans deux variables x et y.
- si le point de coordonnées (x,y) est compris dans le quart de disque centré sur l'origine et de rayon 1, on incrémente alors un compteur c.
- dans tous les cas, on incrémente le compteur de points tirés n.
On obtient alors en calculant 4*c/n une valeur approchée de π .
Remarque: pour calculer un nombre aléatoire entre 0 et 1, utiliser:
1.0*rand()/RAND_MAX
Pour plus de détails, https://www.tutorialspoint.com/c_standard_library/c_function_rand.htm
Exercice 9
crible d’Erathothène
une fonction (procédure) capable d’afficher les nombres premiers compris entre 0 et n.
On pourra utiliser le crible d’Erathostène (https://fr.wikipedia.org/wiki/Crible_d'ératosthène).