Cours:TP M1102 TP 3 Corr : Différence entre versions
m (→Deuxième partie) |
m (→Exercice 4) |
||
| Ligne 469 : | Ligne 469 : | ||
==Exercice 4== | ==Exercice 4== | ||
La synthèse en MUX n'a pas beaucoup d'intérêt avec les FPGA. | La synthèse en MUX n'a pas beaucoup d'intérêt avec les FPGA. | ||
| + | |||
| + | Pour ceux qui voudraient s'y lancer, nous vous rappelons que le principe est le suivant : | ||
| + | *On câble les entrées sur les entrées de sélections (ici "sel") | ||
| + | *on met les 1 et 0 sur les entrées 8 entrées du multiplexeur dans l'ordre de la table de vérité si nos poids sur "sel" ont été choisi dans le même ordre que le table de vérité. | ||
Version du 25 septembre 2020 à 16:50
Il s’agit d’une page protégée.
Sommaire
TP 3
Exercice 1
Question 1
La table de vérité donnée dans wikipédia est :
| A | B | Cin | S | Cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Nous allons la modifier légèrement pour ses entrées et sorties : les 3 entrées sont regroupées et les 2 sorties sont aussi regroupées ensemble
- Table de vérité
Entrées Sorties e(2)=Cin e(1)=B e(0)=A S(1)=Cout S(0)=S 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1
ATTENTION : Nous avons aussi volontairement changé l'ordre ses entrées et des sorties.Il est préférable d'avoir les sorties dans ce sens pour avoir le poids fort des deux bits de sortie à gauche. Pour les entrées c'est moins important.
Voici le fichier VHDL correspondant :
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
ENTITY add1bit IS PORT(
e : in std_logic_vector(2 downto 0); -- Cin, B, A
s : out std_logic_vector(1 downto 0)); -- Cout, S
END add1bit;
ARCHITECTURE arch of add1bit IS
BEGIN
with e select
S <= "00" when "000", --0+0+0=00
"01" when "001", --0+0+1=01
"01" when "010", --0+1+0=01
"10" when "011", --0+1+1=10
"01" when "100", --1+0+0=01
"10" when "101", --1+0+1=10
"10" when "110", --1+1+0=10
"11" when others;--1+1+1=11
END arch;
Question 2
Il faut déjà définir les entrées et sorties de notre problème, autrement dit définir l'entité. Parmi les diverses solutions possibles, nous allons choisir
library IEEE;
use IEEE.std_logic_1164.all;
--use IEEE.std_logic_arith.all;
--use IEEE.STD_LOGIC_UNSIGNED.all;
ENTITY add4 IS
PORT (A,B : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
Cin : IN STD_LOGIC; --retenue entrée dans le schéma
S : OUT STD_LOGIC_VECTOR(4 DOWNTO 0)); --retenue en S(4)
END add4;
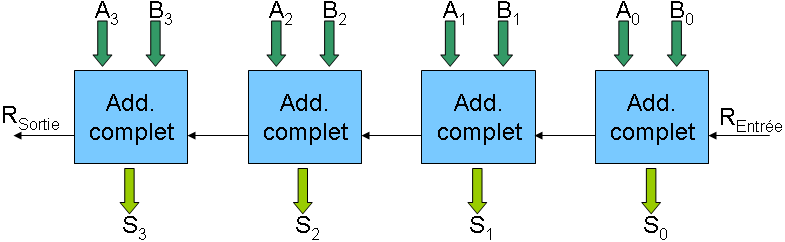
Si l'on compare au schéma de l'énoncé :
on impose ainsi les correspondances suivantes :
Schéma <-> VHDL
- REntrée <-> Cin
- A3 <-> A(3)
- A2 <-> A(2)
- A1 <-> A(1)
- A0 <-> A(0)
- B3 <-> B(3)
- B2 <-> B(2)
- B1 <-> B(1)
- B0 <-> B(0)
- RSortie <-> S(4)
- S3 <-> S(3)
- S2 <-> S(2)
- S1 <-> S(1)
- S0 <-> S(0)
Le programme VHDL devient :
library IEEE;
use IEEE.std_logic_1164.all;
--use IEEE.std_logic_arith.all;
--use IEEE.STD_LOGIC_UNSIGNED.all;
ENTITY add4 IS
PORT (A,B : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
Cin : IN STD_LOGIC; --retenue entrée dans le schéma
S : OUT STD_LOGIC_VECTOR(4 DOWNTO 0)); --retenue en S(4)
END add4;
ARCHITECTURE arch_add4 of add4 IS
COMPONENT add1bit IS PORT(
e : in std_logic_vector(2 downto 0); -- Cin, B, A
s : out std_logic_vector(1 downto 0)); -- Cout, S
END COMPONENT add1bit;
SIGNAL R1, R2, R3 : std_logic; --fils internes non nommés dans le schéma : R1 à droite
BEGIN
i0: add1bit PORT MAP(
e(2) => Cin,
e(1) => B(0),
e(0) => A(0),
S(1) => R1,
S(0) => S(0)); --Il n'y a aucune ambiguité pour VHDL ici
i1: add1bit PORT MAP(
e(2) => R1,
e(1) => B(1),
e(0) => A(1),
S(1) => R2,
S(0) => S(1));
i2: add1bit PORT MAP(
e(2) => R2,
e(1) => B(2),
e(0) => A(2),
S(1) => R3,
S(0) => S(2));
i3: add1bit PORT MAP(
e(2) => R3,
e(1) => B(3),
e(0) => A(3),
S(1) => S(4),
S(0) => S(1));
END arch_add4
--******** Composant à câbler *********
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
ENTITY add1bit IS PORT(
e : in std_logic_vector(2 downto 0); -- Cin, B, A
s : out std_logic_vector(1 downto 0)); -- Cout, S
END add1bit;
ARCHITECTURE arch of add1bit IS
BEGIN
with e select
S <= "00" when "000", --0+0+0=00
"01" when "001", --0+0+1=01
"01" when "010", --0+1+0=01
"10" when "011", --0+1+1=10
"01" when "100", --1+0+0=01
"10" when "101", --1+0+1=10
"10" when "110", --1+1+0=10
"11" when others;--1+1+1=11
END arch;
Le fichier de contraintes peut être simpllifié à :
To,Direction,Location,I/O Bank,VREF Group,Fitter Location,I/O Standard,Reserved,Current Strength,Slew Rate,Differential Pair,Strict Preservation A[0],Unknown,PIN_C10,7,B7_N0,PIN_C10,3.3-V LVTTL,,,,, A[1],Unknown,PIN_C11,7,B7_N0,PIN_C11,3.3-V LVTTL,,,,, A[2],Unknown,PIN_D12,7,B7_N0,,3.3-V LVTTL,,,,, A[3],Unknown,PIN_C12,7,B7_N0,,3.3-V LVTTL,,,,, B[0],Unknown,PIN_A12,7,B7_N0,,3.3-V LVTTL,,,,, B[1],Unknown,PIN_B12,7,B7_N0,,3.3-V LVTTL,,,,, B[2],Unknown,PIN_A13,7,B7_N0,,3.3-V LVTTL,,,,, B[3],Unknown,PIN_A14,7,B7_N0,,3.3-V LVTTL,,,,, Cin,Unknown,PIN_B14,7,B7_N0,,3.3-V LVTTL,,,,, S[0],Unknown,PIN_A8,7,B7_N0,PIN_A8,3.3-V LVTTL,,,,, S[1],Unknown,PIN_A9,7,B7_N0,,3.3-V LVTTL,,,,, S[2],Unknown,PIN_A10,7,B7_N0,,3.3-V LVTTL,,,,, S[3],Unknown,PIN_B10,7,B7_N0,,3.3-V LVTTL,,,,, S[4],Unknown,PIN_D13,7,B7_N0,,3.3-V LVTTL,,,,,
Exercice 2
Il n'est pas inutile de comprendre ce que fait le schéma de l'énoncé, en particulier la présence des OU EXCLUSIFs.
- Passer du binaire au code EXCESS-3 revient à ajouter 3, d'où la présence de l'additionneur avec les entrées (B3,B2,B1,B0) fixées à (GND,GND,Vcc,Vcc) c'est à dire (0,0,1,1)2 c'est à dire 3. C'est vrai que l'on passe à travers des OU EXCLUSIFs mais si vous mettez le Cin Global à 0 les OU EXCLUSIFS sont équivalents à des fils simples !!!!
- Si vous mettez le Cin Global à 1, les OU EXCLUSIFS sont équivalents à des inverseurs logiques ce qui rentre donc dans (B3,B2,B1,B0) est (0,0,1,1)2 c'est à dire le complément bit à bit de 310 + la retenue Cin = 1. On fait donc un complément logique bit à bit auquel on ajoute un et cela s'appelle un complément à deux qui revient à faire une soustraction.
Comme d'habitude la résolution du problème passe par la définition des entrées/sorties c'est à dire de l'entité. On vous propose donc l'entité suivante :
library IEEE;
use IEEE.std_logic_1164.all;
ENTITY XS3Reversible IS
PORT (E : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
Cin : IN STD_LOGIC; --retenue pour choix du sens de codage
Cout : OUT STD_LOGIC; -- il y a une retenue en sortie de add4 : S(4)
s : OUT STD_LOGIC_VECTOR(3 DOWNTO 0));
END XS3Reversible;
Voici donc le code VHDL global :
library IEEE;
use IEEE.std_logic_1164.all;
--use IEEE.std_logic_arith.all;
--use IEEE.STD_LOGIC_UNSIGNED.all;
ENTITY XS3Reversible IS
PORT (E : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
Cin : IN STD_LOGIC; --retenue pour choix du sens de codage
Cout : OUT STD_LOGIC; -- il y a une retenue en sortie de add4
s : OUT STD_LOGIC_VECTOR(3 DOWNTO 0));
END XS3Reversible;
ARCHITECTURE arch_XS3Reversible OF XS3Reversible IS
--Question 2 de l'exercice 1
COMPONENT add4 IS
PORT (A,B : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
Cin : IN STD_LOGIC; --retenue entrée dans le schéma
S : OUT STD_LOGIC_VECTOR(4 DOWNTO 0)); --retenue en S(4)
END COMPONENT add4;
-- fils internes entre les sorties des ou exclusifs et les entrées B(i) de l'additionneur
SIGNAL s_B : STD_LOGIC_VECTOR(3 DOWNTO 0);
BEGIN
-- Fabrication des fils internes avec les OU EXCLUSIFs
s_B(0) <= B(0) XOR Cin;
s_B(1) <= B(0) XOR Cin;
s_B(2) <= B(2) XOR Cin;
s_B(3) <= B(3) XOR Cin;
-- cablage du 7483 = add4
i0: add4 PORT MAP(
A => E,
B => s_B,
Cin => Cin,
S(3 DOWNTO 0) => S,
S(4) => Cout);
END arch_XS3Reversible;
auquel vous ajoutez votre code de l'exercice 1 (question 2) ou le code plus compact de l'énoncé qui a la même entité.
Le fichier de contrainte peut être simplifié à :
To,Direction,Location,I/O Bank,VREF Group,Fitter Location,I/O Standard,Reserved,Current Strength,Slew Rate,Differential Pair,Strict Preservation E[0],Unknown,PIN_C10,7,B7_N0,PIN_C10,3.3-V LVTTL,,,,, E[1],Unknown,PIN_C11,7,B7_N0,PIN_C11,3.3-V LVTTL,,,,, E[2],Unknown,PIN_D12,7,B7_N0,,3.3-V LVTTL,,,,, E[3],Unknown,PIN_C12,7,B7_N0,,3.3-V LVTTL,,,,, Cin,Unknown,PIN_A12,7,B7_N0,,3.3-V LVTTL,,,,, S[0],Unknown,PIN_A8,7,B7_N0,PIN_A8,3.3-V LVTTL,,,,, S[1],Unknown,PIN_A9,7,B7_N0,,3.3-V LVTTL,,,,, S[2],Unknown,PIN_A10,7,B7_N0,,3.3-V LVTTL,,,,, S[3],Unknown,PIN_B10,7,B7_N0,,3.3-V LVTTL,,,,, Cout,Unknown,PIN_D13,7,B7_N0,,3.3-V LVTTL,,,,,
Exercice 3
Première partie
Le comparateur très simplifié est donné maintenant :
library IEEE;
use IEEE.STD_LOGIC_1164.all;
use ieee.std_logic_unsigned.all;
entity COMPM4_exo3 is
port(
GT : out std_logic;
LT : out std_logic;
A : in std_logic_vector(3 downto 0);
B : in std_logic_vector(3 downto 0);
);
end COMPM4_exo3;
architecture COMPM4_exo3_V of COMPM4_exo3 is
begin
GT <= '1' when (A > B ) else '0';
LT <= '1' when (A < B) else '0';
end COMPM4_exo3_V;
Ce comparateur peut être essayé tout seul avec le fichier de contraintes :
To,Direction,Location,I/O Bank,VREF Group,Fitter Location,I/O Standard,Reserved,Current Strength,Slew Rate,Differential Pair,Strict Preservation A[0],Unknown,PIN_C10,7,B7_N0,PIN_C10,3.3-V LVTTL,,,,, A[1],Unknown,PIN_C11,7,B7_N0,PIN_C11,3.3-V LVTTL,,,,, A[2],Unknown,PIN_D12,7,B7_N0,,3.3-V LVTTL,,,,, A[3],Unknown,PIN_C12,7,B7_N0,,3.3-V LVTTL,,,,, B[0],Unknown,PIN_A12,7,B7_N0,,3.3-V LVTTL,,,,, B[1],Unknown,PIN_B12,7,B7_N0,,3.3-V LVTTL,,,,, B[2],Unknown,PIN_A13,7,B7_N0,,3.3-V LVTTL,,,,, B[3],Unknown,PIN_A14,7,B7_N0,,3.3-V LVTTL,,,,, GT,Unknown,PIN_A8,7,B7_N0,PIN_A8,3.3-V LVTTL,,,,, LT,Unknown,PIN_A9,7,B7_N0,,3.3-V LVTTL,,,,,
Deuxième partie
- Table de vérité du comparateur à 9
Entrées Sorties A3 A2 A1 A0 GT 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 0 0 0 0 1 0 0 1 0 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1
Le programme VHDL est donc :
library ieee;
use ieee.std_logic_1164.all;
--use ieee.std_logic_arith.all;
--use ieee.std_logic_unsigned.all;
entity comp9 is port(
A : in std_logic_vector(3 downto 0); -- 8 entrées pour deux digits en entree
GT out std_logic); -- deux digits de 7 segments en sortie
end exo4a;
ARCHITECTURE behavior OF comp9 IS
BEGIN
with A select
GT <= '1' WHEN "1010"|"1011"|"1100"|"1101"|"1110"|"1111",
'0' WHEN OTHERS;
END behavior;
Maintenant pour l'équation simplifiée, on remplit le tableau de Karnaugh :
| S | A1 A0 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|---|
| A3 A2 | \ | ||||
| 00 | 0 | 0 | 0 | 0 | |
| 01 | 0 | 0 | 0 | 0 | |
| 11 | 1 | 1 | 1 | 1 | |
| 10 | 0 | 0 | 1 | 1 |
Ce tableau de Karnaugh donne l'équation simplifiée : GT = A3.A2 + A3.A1
Soit en VHDL :
library ieee;
use ieee.std_logic_1164.all;
--use ieee.std_logic_arith.all;
--use ieee.std_logic_unsigned.all;
entity comp9 is port(
A : in std_logic_vector(3 downto 0); -- 8 entrées pour deux digits en entree
GT out std_logic); -- deux digits de 7 segments en sortie
end exo4a;
ARCHITECTURE behavior OF comp9 IS
BEGIN
GT <= (A(3) AND A(2)) OR (A(3) AND A(1));
END behavior;
Exercice 4
La synthèse en MUX n'a pas beaucoup d'intérêt avec les FPGA.
Pour ceux qui voudraient s'y lancer, nous vous rappelons que le principe est le suivant :
- On câble les entrées sur les entrées de sélections (ici "sel")
- on met les 1 et 0 sur les entrées 8 entrées du multiplexeur dans l'ordre de la table de vérité si nos poids sur "sel" ont été choisi dans le même ordre que le table de vérité.