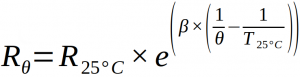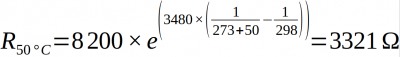Cours:ArduinoTemperature

Mesure de température par CTN

Principe

Pour mesurer la température nous allons utiliser une thermistance CTN. Une thermistance est une résistance dont sa valeur dépend de la température.

Ici on va utiliser une CTN (coefficient de température négative) la résistance diminue quand la température augmente. Une CTP (coefficient de température positive) la résistance augmente quand la température augmente.

Symbole du composant	Valeur de la résistance en fct de la température pour une CTN

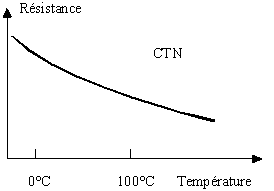
On constate sur la courbe précédente que la valeur de la CTN n'est pas linéaire en fonction de la température.

Utilisation

Les thermistances sont utilisées pour la mesure de température ou la compensation dans une grande variété d'applications.

Exemple :

Contrôle de la température dans les appareils de communication mobile :

L'utilisation d'appareils de communication mobiles dans une large plage de températures nécessite le contrôle des éléments sensibles à la température du système. Ceci comprend l'oscillateur à cristal, l'écran LCD, l'amplificateur de puissance et la batterie. Les thermistances remplissent différentes tâches, par ex. compensation de température ou détection de température dans un circuit de protection contre la surchauffe. (note d’application)

Pont diviseur

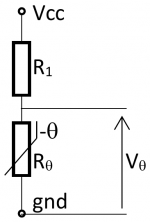
On place la CTN dans un pont diviseur (cf figure ci dessous).

1. Lorsque la température change :
2. la valeur de la CTN change
3. donc la tension Vθ change
4. on mesure cette tension qui permet d'en déduire la valeur de la température.

R1 résistance fixe Rθ résistance variable en fonction de la température Vθ tension image de la température Vcc tension d’alimentation du montage gnd tension de référence (masse 0V)

Etape 1 : relation V_θ=f(R_θ)

Exprimez la relation entre

Vθ = f(Vcc, R1 et Rθ)

Remarque :

• θ est la température, exprimée en Kelvin

Etape 2 : caractéristique résistance / température

On considère que sur une plage de température, la résistance de la thermistance est :

avec R_25°C = 8200Ω, β = 3480 K, T_25°C = 273+25 et θ exprimée en Kelvin

Exemple : pour θ = 50°C

En utilisant la feuille de calculs suivante, déterminez la résistance de la CTN sur la plage de température. On rappelle que la fonction exponentielle est EXP.

lien vers la feuille

La résistance R1 (12 k), en utilisant la feuille de calculs du fichier, déterminez :

la tension Vθ sur la plage de température avec Vcc = 5 V

Etape 3 : Conversion de la tension en nombre numérique puis en température

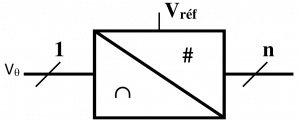
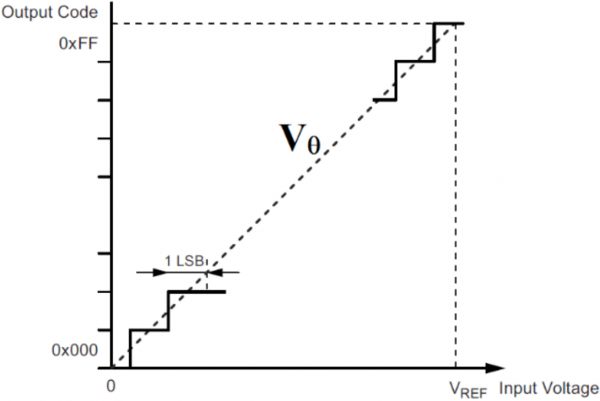
Principe de fonctionnement du CAN

On entre une tension analogique V_θ et on ressort un nombre numérique en binaire sous n fils suivant la résolution du CAN.

Exemple pour la carte NANO

• La résolution n peut être de 10 bits ou de 8 bits soit 1024 ou 256 combinaisons.
• La tension de référence Vréf est soit de 5V soit de 1,1V

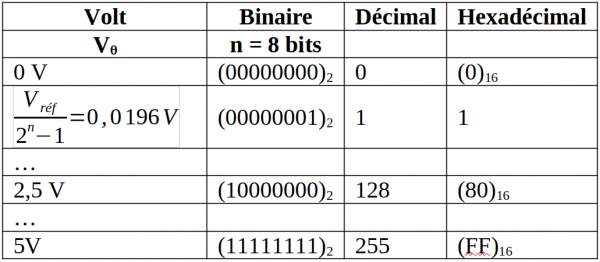
Pour Vréf = 5V :

La tension de 0,0196 V est appelée le quantum. On a une résolution de 20 mV

Quand la tension analogique Vθ varie linéairement de 0 à Vréf la valeur numérique évolue en palier de 0 à 255 en pas d’un quantum soit environ 20 mV. Le quantum est aussi appelé le LSB le bit le moins significatif (Least Significant Bit).

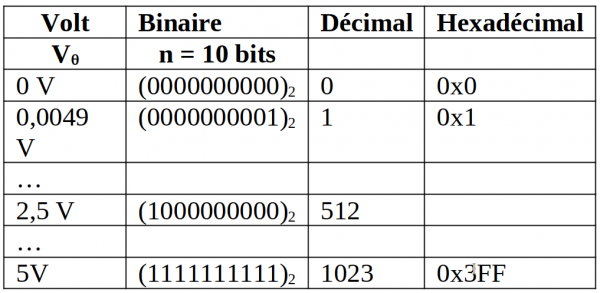
Pour n = 10 bits

En utilisant n = 10 bits la résolution est meilleure car le quantum est de 5 mV mais le temps de conversion est plus long. Pour la tension de référence de 1,1V on remplace simplement la colonne Volt de 0 à 1,1 V, au-delà de 1,1 V jusqu’à 5V, le convertisseur est saturé, la valeur numérique reste constante à 255 ou 1023 suivant la résolution 8 ou 10 bits. Le quantum sera respectivement de 4,3 mV et 1 mV environ.

Déterminer la valeur de la résistance R1 pour la plage de température afin que la tension V ne dépasse pas la tension de référence de 1,1 V.

Maintenant déterminons la température en fonction de la valeur numérique du convertisseur

Dans le premier saé nous avions affiché l’image de la température en volt. Maintenant nous somme en mesure après quelques petits calculs d’afficher la température en degré Celsius.

Exprimez la température θ en utilisant la formule :

Pour déterminer la température θ il nous faut R_θ qui est l’inconnu dans l’équation.

Exprimez : la résistance Rθ en utilisant la formule Vθ = f(Vcc, R1 et Rθ).trouvée à la première question.

Sachant que la valeur numérique N=V_θ/q avec q=Vref/(2ⁿ-1) le quantum et n la résolution du CAN (8 ou 10 bits)

Exprimez la formule de la température en degré Celsius en fonction de la valeur N du convertisseur analogique.