Cours:TP M1102 TP 3 Corr : Différence entre versions
m (→Exercice 4) |
m (→Exercice 4) |
||
| Ligne 473 : | Ligne 473 : | ||
*On câble les entrées sur les entrées de sélections (ici "sel") | *On câble les entrées sur les entrées de sélections (ici "sel") | ||
*on met les 1 et 0 sur les entrées 8 entrées du multiplexeur dans l'ordre de la table de vérité si nos poids sur "sel" ont été choisi dans le même ordre que le table de vérité. | *on met les 1 et 0 sur les entrées 8 entrées du multiplexeur dans l'ordre de la table de vérité si nos poids sur "sel" ont été choisi dans le même ordre que le table de vérité. | ||
| + | |||
| + | Par exemple, | ||
| + | ; Table de vérité | ||
| + | :{| border cellspacing="0" width="150" | ||
| + | |- style = "background:#b3e2d1;text-align:center" | ||
| + | | colspan="3"|Entrées||colspan="2"|Sorties | ||
| + | |- style="text-align:center" | ||
| + | |'''e(2)=C<sub>in</sub>'''||'''e(1)=B'''||'''e(0)=A'''||'''S(1)=C<sub>out</sub>'''||'''S(0)=S''' | ||
| + | |- style="text-align:center" | ||
| + | ||0||0||0||'''0'''||'''0''' | ||
| + | |- style="text-align:center" | ||
| + | ||0||0||1||'''0'''||'''1''' | ||
| + | |- style="text-align:center" | ||
| + | ||0||1||0||'''0'''||'''1''' | ||
| + | |- style="text-align:center" | ||
| + | ||0||1||1||'''1'''||'''0''' | ||
| + | |- style="text-align:center" | ||
| + | ||1||0||0||'''0'''||'''1''' | ||
| + | |- style="text-align:center" | ||
| + | ||1||0||1||'''1'''||'''0''' | ||
| + | |- style="text-align:center" | ||
| + | ||1||1||0||'''1'''||'''0''' | ||
| + | |- style="text-align:center" | ||
| + | ||1||1||1||'''1'''||'''1''' | ||
| + | |} | ||
| + | |||
| + | sera réalisé en câblant e(2) sur sel(2), e(1) sur sel(1) et e(0) sur sel(0) pour les deux multiplexeurs (ben oui il y a deux sorties donc deux multiplexeurs). | ||
| + | |||
| + | Alors la première colonne S(1) de la table de vérité ira dans l'ordre sur e(0),e(1),...,e(7) tandis que la deuxième colonne S(0) de la table de vérité ira dans l'ordre sur e(0),e(1),...,e(7) du deuxième mux. | ||
Version du 25 septembre 2020 à 16:57
Il s’agit d’une page protégée.
Sommaire
TP 3
Exercice 1
Question 1
La table de vérité donnée dans wikipédia est :
| A | B | Cin | S | Cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Nous allons la modifier légèrement pour ses entrées et sorties : les 3 entrées sont regroupées et les 2 sorties sont aussi regroupées ensemble
- Table de vérité
Entrées Sorties e(2)=Cin e(1)=B e(0)=A S(1)=Cout S(0)=S 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1
ATTENTION : Nous avons aussi volontairement changé l'ordre ses entrées et des sorties.Il est préférable d'avoir les sorties dans ce sens pour avoir le poids fort des deux bits de sortie à gauche. Pour les entrées c'est moins important.
Voici le fichier VHDL correspondant :
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
ENTITY add1bit IS PORT(
e : in std_logic_vector(2 downto 0); -- Cin, B, A
s : out std_logic_vector(1 downto 0)); -- Cout, S
END add1bit;
ARCHITECTURE arch of add1bit IS
BEGIN
with e select
S <= "00" when "000", --0+0+0=00
"01" when "001", --0+0+1=01
"01" when "010", --0+1+0=01
"10" when "011", --0+1+1=10
"01" when "100", --1+0+0=01
"10" when "101", --1+0+1=10
"10" when "110", --1+1+0=10
"11" when others;--1+1+1=11
END arch;
Question 2
Il faut déjà définir les entrées et sorties de notre problème, autrement dit définir l'entité. Parmi les diverses solutions possibles, nous allons choisir
library IEEE;
use IEEE.std_logic_1164.all;
--use IEEE.std_logic_arith.all;
--use IEEE.STD_LOGIC_UNSIGNED.all;
ENTITY add4 IS
PORT (A,B : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
Cin : IN STD_LOGIC; --retenue entrée dans le schéma
S : OUT STD_LOGIC_VECTOR(4 DOWNTO 0)); --retenue en S(4)
END add4;
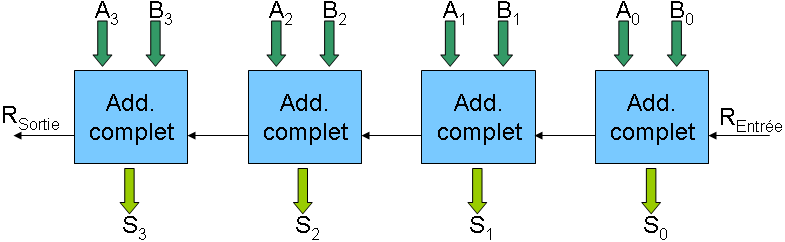
Si l'on compare au schéma de l'énoncé :
on impose ainsi les correspondances suivantes :
Schéma <-> VHDL
- REntrée <-> Cin
- A3 <-> A(3)
- A2 <-> A(2)
- A1 <-> A(1)
- A0 <-> A(0)
- B3 <-> B(3)
- B2 <-> B(2)
- B1 <-> B(1)
- B0 <-> B(0)
- RSortie <-> S(4)
- S3 <-> S(3)
- S2 <-> S(2)
- S1 <-> S(1)
- S0 <-> S(0)
Le programme VHDL devient :
library IEEE;
use IEEE.std_logic_1164.all;
--use IEEE.std_logic_arith.all;
--use IEEE.STD_LOGIC_UNSIGNED.all;
ENTITY add4 IS
PORT (A,B : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
Cin : IN STD_LOGIC; --retenue entrée dans le schéma
S : OUT STD_LOGIC_VECTOR(4 DOWNTO 0)); --retenue en S(4)
END add4;
ARCHITECTURE arch_add4 of add4 IS
COMPONENT add1bit IS PORT(
e : in std_logic_vector(2 downto 0); -- Cin, B, A
s : out std_logic_vector(1 downto 0)); -- Cout, S
END COMPONENT add1bit;
SIGNAL R1, R2, R3 : std_logic; --fils internes non nommés dans le schéma : R1 à droite
BEGIN
i0: add1bit PORT MAP(
e(2) => Cin,
e(1) => B(0),
e(0) => A(0),
S(1) => R1,
S(0) => S(0)); --Il n'y a aucune ambiguité pour VHDL ici
i1: add1bit PORT MAP(
e(2) => R1,
e(1) => B(1),
e(0) => A(1),
S(1) => R2,
S(0) => S(1));
i2: add1bit PORT MAP(
e(2) => R2,
e(1) => B(2),
e(0) => A(2),
S(1) => R3,
S(0) => S(2));
i3: add1bit PORT MAP(
e(2) => R3,
e(1) => B(3),
e(0) => A(3),
S(1) => S(4),
S(0) => S(1));
END arch_add4
--******** Composant à câbler *********
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
ENTITY add1bit IS PORT(
e : in std_logic_vector(2 downto 0); -- Cin, B, A
s : out std_logic_vector(1 downto 0)); -- Cout, S
END add1bit;
ARCHITECTURE arch of add1bit IS
BEGIN
with e select
S <= "00" when "000", --0+0+0=00
"01" when "001", --0+0+1=01
"01" when "010", --0+1+0=01
"10" when "011", --0+1+1=10
"01" when "100", --1+0+0=01
"10" when "101", --1+0+1=10
"10" when "110", --1+1+0=10
"11" when others;--1+1+1=11
END arch;
Le fichier de contraintes peut être simpllifié à :
To,Direction,Location,I/O Bank,VREF Group,Fitter Location,I/O Standard,Reserved,Current Strength,Slew Rate,Differential Pair,Strict Preservation A[0],Unknown,PIN_C10,7,B7_N0,PIN_C10,3.3-V LVTTL,,,,, A[1],Unknown,PIN_C11,7,B7_N0,PIN_C11,3.3-V LVTTL,,,,, A[2],Unknown,PIN_D12,7,B7_N0,,3.3-V LVTTL,,,,, A[3],Unknown,PIN_C12,7,B7_N0,,3.3-V LVTTL,,,,, B[0],Unknown,PIN_A12,7,B7_N0,,3.3-V LVTTL,,,,, B[1],Unknown,PIN_B12,7,B7_N0,,3.3-V LVTTL,,,,, B[2],Unknown,PIN_A13,7,B7_N0,,3.3-V LVTTL,,,,, B[3],Unknown,PIN_A14,7,B7_N0,,3.3-V LVTTL,,,,, Cin,Unknown,PIN_B14,7,B7_N0,,3.3-V LVTTL,,,,, S[0],Unknown,PIN_A8,7,B7_N0,PIN_A8,3.3-V LVTTL,,,,, S[1],Unknown,PIN_A9,7,B7_N0,,3.3-V LVTTL,,,,, S[2],Unknown,PIN_A10,7,B7_N0,,3.3-V LVTTL,,,,, S[3],Unknown,PIN_B10,7,B7_N0,,3.3-V LVTTL,,,,, S[4],Unknown,PIN_D13,7,B7_N0,,3.3-V LVTTL,,,,,
Exercice 2
Il n'est pas inutile de comprendre ce que fait le schéma de l'énoncé, en particulier la présence des OU EXCLUSIFs.
- Passer du binaire au code EXCESS-3 revient à ajouter 3, d'où la présence de l'additionneur avec les entrées (B3,B2,B1,B0) fixées à (GND,GND,Vcc,Vcc) c'est à dire (0,0,1,1)2 c'est à dire 3. C'est vrai que l'on passe à travers des OU EXCLUSIFs mais si vous mettez le Cin Global à 0 les OU EXCLUSIFS sont équivalents à des fils simples !!!!
- Si vous mettez le Cin Global à 1, les OU EXCLUSIFS sont équivalents à des inverseurs logiques ce qui rentre donc dans (B3,B2,B1,B0) est (0,0,1,1)2 c'est à dire le complément bit à bit de 310 + la retenue Cin = 1. On fait donc un complément logique bit à bit auquel on ajoute un et cela s'appelle un complément à deux qui revient à faire une soustraction.
Comme d'habitude la résolution du problème passe par la définition des entrées/sorties c'est à dire de l'entité. On vous propose donc l'entité suivante :
library IEEE;
use IEEE.std_logic_1164.all;
ENTITY XS3Reversible IS
PORT (E : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
Cin : IN STD_LOGIC; --retenue pour choix du sens de codage
Cout : OUT STD_LOGIC; -- il y a une retenue en sortie de add4 : S(4)
s : OUT STD_LOGIC_VECTOR(3 DOWNTO 0));
END XS3Reversible;
Voici donc le code VHDL global :
library IEEE;
use IEEE.std_logic_1164.all;
--use IEEE.std_logic_arith.all;
--use IEEE.STD_LOGIC_UNSIGNED.all;
ENTITY XS3Reversible IS
PORT (E : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
Cin : IN STD_LOGIC; --retenue pour choix du sens de codage
Cout : OUT STD_LOGIC; -- il y a une retenue en sortie de add4
s : OUT STD_LOGIC_VECTOR(3 DOWNTO 0));
END XS3Reversible;
ARCHITECTURE arch_XS3Reversible OF XS3Reversible IS
--Question 2 de l'exercice 1
COMPONENT add4 IS
PORT (A,B : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
Cin : IN STD_LOGIC; --retenue entrée dans le schéma
S : OUT STD_LOGIC_VECTOR(4 DOWNTO 0)); --retenue en S(4)
END COMPONENT add4;
-- fils internes entre les sorties des ou exclusifs et les entrées B(i) de l'additionneur
SIGNAL s_B : STD_LOGIC_VECTOR(3 DOWNTO 0);
BEGIN
-- Fabrication des fils internes avec les OU EXCLUSIFs
s_B(0) <= B(0) XOR Cin;
s_B(1) <= B(0) XOR Cin;
s_B(2) <= B(2) XOR Cin;
s_B(3) <= B(3) XOR Cin;
-- cablage du 7483 = add4
i0: add4 PORT MAP(
A => E,
B => s_B,
Cin => Cin,
S(3 DOWNTO 0) => S,
S(4) => Cout);
END arch_XS3Reversible;
auquel vous ajoutez votre code de l'exercice 1 (question 2) ou le code plus compact de l'énoncé qui a la même entité.
Le fichier de contrainte peut être simplifié à :
To,Direction,Location,I/O Bank,VREF Group,Fitter Location,I/O Standard,Reserved,Current Strength,Slew Rate,Differential Pair,Strict Preservation E[0],Unknown,PIN_C10,7,B7_N0,PIN_C10,3.3-V LVTTL,,,,, E[1],Unknown,PIN_C11,7,B7_N0,PIN_C11,3.3-V LVTTL,,,,, E[2],Unknown,PIN_D12,7,B7_N0,,3.3-V LVTTL,,,,, E[3],Unknown,PIN_C12,7,B7_N0,,3.3-V LVTTL,,,,, Cin,Unknown,PIN_A12,7,B7_N0,,3.3-V LVTTL,,,,, S[0],Unknown,PIN_A8,7,B7_N0,PIN_A8,3.3-V LVTTL,,,,, S[1],Unknown,PIN_A9,7,B7_N0,,3.3-V LVTTL,,,,, S[2],Unknown,PIN_A10,7,B7_N0,,3.3-V LVTTL,,,,, S[3],Unknown,PIN_B10,7,B7_N0,,3.3-V LVTTL,,,,, Cout,Unknown,PIN_D13,7,B7_N0,,3.3-V LVTTL,,,,,
Exercice 3
Première partie
Le comparateur très simplifié est donné maintenant :
library IEEE;
use IEEE.STD_LOGIC_1164.all;
use ieee.std_logic_unsigned.all;
entity COMPM4_exo3 is
port(
GT : out std_logic;
LT : out std_logic;
A : in std_logic_vector(3 downto 0);
B : in std_logic_vector(3 downto 0);
);
end COMPM4_exo3;
architecture COMPM4_exo3_V of COMPM4_exo3 is
begin
GT <= '1' when (A > B ) else '0';
LT <= '1' when (A < B) else '0';
end COMPM4_exo3_V;
Ce comparateur peut être essayé tout seul avec le fichier de contraintes :
To,Direction,Location,I/O Bank,VREF Group,Fitter Location,I/O Standard,Reserved,Current Strength,Slew Rate,Differential Pair,Strict Preservation A[0],Unknown,PIN_C10,7,B7_N0,PIN_C10,3.3-V LVTTL,,,,, A[1],Unknown,PIN_C11,7,B7_N0,PIN_C11,3.3-V LVTTL,,,,, A[2],Unknown,PIN_D12,7,B7_N0,,3.3-V LVTTL,,,,, A[3],Unknown,PIN_C12,7,B7_N0,,3.3-V LVTTL,,,,, B[0],Unknown,PIN_A12,7,B7_N0,,3.3-V LVTTL,,,,, B[1],Unknown,PIN_B12,7,B7_N0,,3.3-V LVTTL,,,,, B[2],Unknown,PIN_A13,7,B7_N0,,3.3-V LVTTL,,,,, B[3],Unknown,PIN_A14,7,B7_N0,,3.3-V LVTTL,,,,, GT,Unknown,PIN_A8,7,B7_N0,PIN_A8,3.3-V LVTTL,,,,, LT,Unknown,PIN_A9,7,B7_N0,,3.3-V LVTTL,,,,,
Deuxième partie
- Table de vérité du comparateur à 9
Entrées Sorties A3 A2 A1 A0 GT 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 0 0 0 0 1 0 0 1 0 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1
Le programme VHDL est donc :
library ieee;
use ieee.std_logic_1164.all;
--use ieee.std_logic_arith.all;
--use ieee.std_logic_unsigned.all;
entity comp9 is port(
A : in std_logic_vector(3 downto 0); -- 8 entrées pour deux digits en entree
GT out std_logic); -- deux digits de 7 segments en sortie
end exo4a;
ARCHITECTURE behavior OF comp9 IS
BEGIN
with A select
GT <= '1' WHEN "1010"|"1011"|"1100"|"1101"|"1110"|"1111",
'0' WHEN OTHERS;
END behavior;
Maintenant pour l'équation simplifiée, on remplit le tableau de Karnaugh :
| S | A1 A0 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|---|
| A3 A2 | \ | ||||
| 00 | 0 | 0 | 0 | 0 | |
| 01 | 0 | 0 | 0 | 0 | |
| 11 | 1 | 1 | 1 | 1 | |
| 10 | 0 | 0 | 1 | 1 |
Ce tableau de Karnaugh donne l'équation simplifiée : GT = A3.A2 + A3.A1
Soit en VHDL :
library ieee;
use ieee.std_logic_1164.all;
--use ieee.std_logic_arith.all;
--use ieee.std_logic_unsigned.all;
entity comp9 is port(
A : in std_logic_vector(3 downto 0); -- 8 entrées pour deux digits en entree
GT out std_logic); -- deux digits de 7 segments en sortie
end exo4a;
ARCHITECTURE behavior OF comp9 IS
BEGIN
GT <= (A(3) AND A(2)) OR (A(3) AND A(1));
END behavior;
Exercice 4
La synthèse en MUX n'a pas beaucoup d'intérêt avec les FPGA.
Pour ceux qui voudraient s'y lancer, nous vous rappelons que le principe est le suivant :
- On câble les entrées sur les entrées de sélections (ici "sel")
- on met les 1 et 0 sur les entrées 8 entrées du multiplexeur dans l'ordre de la table de vérité si nos poids sur "sel" ont été choisi dans le même ordre que le table de vérité.
Par exemple,
- Table de vérité
Entrées Sorties e(2)=Cin e(1)=B e(0)=A S(1)=Cout S(0)=S 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1
sera réalisé en câblant e(2) sur sel(2), e(1) sur sel(1) et e(0) sur sel(0) pour les deux multiplexeurs (ben oui il y a deux sorties donc deux multiplexeurs).
Alors la première colonne S(1) de la table de vérité ira dans l'ordre sur e(0),e(1),...,e(7) tandis que la deuxième colonne S(0) de la table de vérité ira dans l'ordre sur e(0),e(1),...,e(7) du deuxième mux.