Cours:Elen4 TNS TP Implementations : Différence entre versions
| (28 révisions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 5 : | Ligne 5 : | ||
</center> | </center> | ||
| − | Le travail de ce TP va consister à filtrer des signaux numériques avec divers | + | Le travail de ce TP va consister à filtrer des signaux numériques avec divers filtres RIF, en exploitant trois implémentations différentes à partir du produit de convolution, de la réponse fréquentielle et de l'équation aux différences. |
| − | |||
| − | |||
L'objectif est de filtrer le signal | L'objectif est de filtrer le signal | ||
| Ligne 30 : | Ligne 28 : | ||
X1 = sin(N/10) + randn(size(N))/3; | X1 = sin(N/10) + randn(size(N))/3; | ||
</source> | </source> | ||
| + | |||
| + | ===== Avec <code>filter</code> ===== | ||
| + | |||
| + | Il est évidemment possible de demander à Matlab de réaliser directement le filtrage, en utilisant la fonction <code>y = filter(b,a,x)</code> qui traite le signal <code>x</code> avec le filtre défini par ses coefficients de sa fonction de transfert (<code>b</code> pour numérateur et <code>a</code> pour le dénominateur). | ||
| + | Voir la documentation (https://fr.mathworks.com/help/matlab/ref/filter.html) pour le détail, en particulier cette partie (https://fr.mathworks.com/help/matlab/ref/filter.html#buaif7c-5) pour le lien entre les tableaux <code>a</code> et <code>b</code> et la fonction de transfert. | ||
| + | |||
| + | Cependant, pour éviter l'effet "boite noire", nous allons voir comment implémenter nous même un filtre. | ||
===== Avec le produit de convolution ===== | ===== Avec le produit de convolution ===== | ||
| Ligne 74 : | Ligne 79 : | ||
Une implémentation en ligne permet de traiter le signal '''pendant ou au cours''' de son acquisition. Il s'agit de calculer à la volée les valeurs du signal de sortie. Il faut pour cela s'appuyer sur l'équation au différence, qui permet d'exprimer ''y(n)''. | Une implémentation en ligne permet de traiter le signal '''pendant ou au cours''' de son acquisition. Il s'agit de calculer à la volée les valeurs du signal de sortie. Il faut pour cela s'appuyer sur l'équation au différence, qui permet d'exprimer ''y(n)''. | ||
| + | |||
| + | ===== Avec un bloc <code>FIR filter</code> ===== | ||
| + | |||
| + | Comme pour Matlab, il est possible d'utiliser un bloc implémentant directement un filtre FIR (''Finite Impulse Response''), il s'agit du bloc <code>Frequency Xlating FIR filter</code>. | ||
| + | |||
| + | Vous pourrez consulter la page [https://wiki.gnuradio.org/index.php/Designing_Filter_Taps Designing Filter Taps], en particulier la section ''Entering Filter Taps Manually''. | ||
===== À partir du schéma-bloc ===== | ===== À partir du schéma-bloc ===== | ||
| Ligne 83 : | Ligne 94 : | ||
c) Dans GnuRadio, produire un schéma qui implémente ce filtre. | c) Dans GnuRadio, produire un schéma qui implémente ce filtre. | ||
| − | * La source sera un bloc <code>Signal Source</code> sinus | + | * La source sera un bloc <code>Signal Source</code> sinus. La fréquence du sinus sera obtenue à partir de la fréquence d'échantillonnage <code>samp_rate</code> et de la définition ''x(n)=sin(n/10)''. On rappelle que ''sin(wt)'' est un sinus de pulsation ''w''. |
* Le bruit sera obtenu par un bloc <code>Noise Source</code> | * Le bruit sera obtenu par un bloc <code>Noise Source</code> | ||
* Vous implémenterez le système à l'aide de <code>Add</code> pour les additionneurs, de <code>Delay</code> pour les retards et de <code>Multiply Const</code> pour les gains | * Vous implémenterez le système à l'aide de <code>Add</code> pour les additionneurs, de <code>Delay</code> pour les retards et de <code>Multiply Const</code> pour les gains | ||
* Vous afficherez les graphes de ''x<sub>1</sub>'' et de la sortie ''y'' avec 200 points (comme pour les implémentations dans Matlab) | * Vous afficherez les graphes de ''x<sub>1</sub>'' et de la sortie ''y'' avec 200 points (comme pour les implémentations dans Matlab) | ||
| + | |||
| + | c) Afin de comparer l'implémentation GnuRadio aux implémentation Matlab, il est nécessaire de travailler sur le même signal : | ||
| + | * Dans Matlab : écrire les valeurs du signal <code>X1</code> dans un fichier : | ||
| + | <source lang=matlab> | ||
| + | f = fopen('x.raw', 'w'); | ||
| + | fwrite(f, x, 'float'); | ||
| + | fclose(f); | ||
| + | </source> | ||
| + | * Dans Gnuradio : utiliser les valeurs du fichier <code>x.raw</code> à l'aide d'un bloc <code>File Source</code> (attention à bien préciser une longueur de 200, des valeurs en 'float' et une non-répétition de la lecture). | ||
| + | * Vous pourrez ensuite utiliser un bloc <code>File Sink</code> ([https://wiki.gnuradio.org/index.php?title=File_Sink File Sink]) pour écrire les valeurs de ''y'' dans un fichier, pour les relire dans Matlab afin de les comparer aux résultats précédents. | ||
===== En écrivant du code ===== | ===== En écrivant du code ===== | ||
| Ligne 96 : | Ligne 117 : | ||
=== Comparaison === | === Comparaison === | ||
| − | Discuter de l’intérêt de chacune des implémentations (convolution, en fréquence, et avec l’équation aux | + | Discuter de l’intérêt de chacune des implémentations (convolution, en fréquence, et avec l’équation aux différences), en termes de complexité de calcul et contrainte d'utilisation (en ligne / hors ligne). |
| − | |||
| − | |||
Version actuelle datée du 20 mars 2023 à 14:58
TP3 : Implémentation des filtres numériques
Le travail de ce TP va consister à filtrer des signaux numériques avec divers filtres RIF, en exploitant trois implémentations différentes à partir du produit de convolution, de la réponse fréquentielle et de l'équation aux différences.
L'objectif est de filtrer le signal
x1(n) = sin(n/10) + b(n)
b(t) étant du bruit gaussien.
Le filtre sera défini par sa fonction de transfert
| H(z) = |
1 + 2z-1 + z-2 |
| | |
|
4 |
Sommaire
Implémentation hors-ligne
Il s'agit de traiter le signal après son acquisition.
Dans Matlab, Vous travaillerez avec le signal x1 créé par le code suivant :
N = 1:200;
X1 = sin(N/10) + randn(size(N))/3;
Avec filter
Il est évidemment possible de demander à Matlab de réaliser directement le filtrage, en utilisant la fonction y = filter(b,a,x) qui traite le signal x avec le filtre défini par ses coefficients de sa fonction de transfert (b pour numérateur et a pour le dénominateur).
Voir la documentation (https://fr.mathworks.com/help/matlab/ref/filter.html) pour le détail, en particulier cette partie (https://fr.mathworks.com/help/matlab/ref/filter.html#buaif7c-5) pour le lien entre les tableaux a et b et la fonction de transfert.
Cependant, pour éviter l'effet "boite noire", nous allons voir comment implémenter nous même un filtre.
Avec le produit de convolution
Avec le produit de convolution, Il s'agit d'une implémentation hors-ligne dans le domaine temporel. On nommera yc le signal de sortie obtenue avec cette implémentation.
a) Appliquez à x1 le filtre RIF dont la fonction de transfert est H(z)
par un produit de convolution (fonction conv()) avec la réponse impusionnelle h du filtre :
yc = x1 ∗ h.
b) Tracer le graphe de l'entrée x1 et de la sortie obtenue :
figure(1)
subplot(211); plot(X1); xlabel(’n’); ylabel(’x1[n]’);
subplot(212); plot(Yc); xlabel(’n’); ylabel(’yc[n] avec conv’);
Avec la réponse fréquentielle
Avec la réponse fréquentielle, il s'agit d'une implémentation hors-ligne dans le domaine fréquentiel. On nommera yf le signal de sortie obtenue avec cette implémentation.
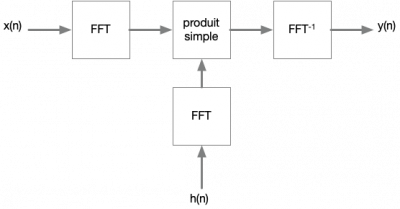
a) En exploitant le théorème de la convolution (le produit de convolution se transforme en produit simple fréquences à fréquences), filtrer le signal x1.
Fig : principe du filtrage dans le domaine fréquentiel.
b) Tracer le spectre d’amplitude de x1, la réponse fréquentielle de H et le spectre d’amplitude de la sortie yc.
Comparaison des implémentations
Vérifier que le filtrage dans le domaine fréquentiel fourni une sortie identique à celle obtenue avec le produit de convolution. Vous pourrez faire
a) une vérification graphique en affichant les signaux yc et yf
b) ainsi qu'une vérification quantifiée en calculant une norme entre les deux signaux y. (todo : faire le lien avec le snr ici ?)
Implémentation en ligne
Une implémentation en ligne permet de traiter le signal pendant ou au cours de son acquisition. Il s'agit de calculer à la volée les valeurs du signal de sortie. Il faut pour cela s'appuyer sur l'équation au différence, qui permet d'exprimer y(n).
Avec un bloc FIR filter
Comme pour Matlab, il est possible d'utiliser un bloc implémentant directement un filtre FIR (Finite Impulse Response), il s'agit du bloc Frequency Xlating FIR filter.
Vous pourrez consulter la page Designing Filter Taps, en particulier la section Entering Filter Taps Manually.
À partir du schéma-bloc
a) Établir l'équation aux différence du filtre H
b) Donner le schéma-bloc équivalent à cette équation aux différences.
c) Dans GnuRadio, produire un schéma qui implémente ce filtre.
- La source sera un bloc
Signal Sourcesinus. La fréquence du sinus sera obtenue à partir de la fréquence d'échantillonnagesamp_rateet de la définition x(n)=sin(n/10). On rappelle que sin(wt) est un sinus de pulsation w. - Le bruit sera obtenu par un bloc
Noise Source - Vous implémenterez le système à l'aide de
Addpour les additionneurs, deDelaypour les retards et deMultiply Constpour les gains - Vous afficherez les graphes de x1 et de la sortie y avec 200 points (comme pour les implémentations dans Matlab)
c) Afin de comparer l'implémentation GnuRadio aux implémentation Matlab, il est nécessaire de travailler sur le même signal :
- Dans Matlab : écrire les valeurs du signal
X1dans un fichier :
f = fopen('x.raw', 'w');
fwrite(f, x, 'float');
fclose(f);
- Dans Gnuradio : utiliser les valeurs du fichier
x.rawà l'aide d'un blocFile Source(attention à bien préciser une longueur de 200, des valeurs en 'float' et une non-répétition de la lecture). - Vous pourrez ensuite utiliser un bloc
File Sink(File Sink) pour écrire les valeurs de y dans un fichier, pour les relire dans Matlab afin de les comparer aux résultats précédents.
En écrivant du code
Dans ce cas, le travail consiste à calculer y(n) à partir de la valeur x(n) et de ses versions précédentes x(n-1) et x(n-2) qu'il est nécessaire de stocker.
Ceci sera mis en place dans un TP ultérieur (Implémentations temps-réel)
Comparaison
Discuter de l’intérêt de chacune des implémentations (convolution, en fréquence, et avec l’équation aux différences), en termes de complexité de calcul et contrainte d'utilisation (en ligne / hors ligne).