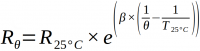Cours:ArduinoTemperature : Différence entre versions

De troyesGEII
Aller à : navigation, rechercher
(→‎Principe)
(→‎Analyse)
 
(22 révisions intermédiaires par le même utilisateur non affichées)
Ligne 30 : Ligne 30 :
 
On constate sur la courbe précédente que la {{Rouge|valeur}} de la CTN n'est {{Rouge|pas linéaire}} en fonction de la température.
 
On constate sur la courbe précédente que la {{Rouge|valeur}} de la CTN n'est {{Rouge|pas linéaire}} en fonction de la température.
  
−
==Utilisation==
+
la mesure de température ou la compensation dans une grande variété d'applications.
  
−
Les thermistances sont utilisées pour la mesure de température ou la compensation dans une grande variété d'applications.
 
  
−
'''Exemple :'''
 
  
−
Contrôle de la température dans les appareils de communication mobile :
+
'''Usage : ''' Les thermistances sont utilisées pour
 +
*la mesure de température
 +
*détection de surchauffe
 +
*la compensation en température ( compensation de la variation de la caractéristique de composants lorsque la température change)
  
−
L'utilisation d'appareils de communication mobiles dans une large plage de températures nécessite le contrôle des éléments sensibles à la température du système. Ceci comprend l'oscillateur à cristal, l'écran LCD, l'amplificateur de puissance et la batterie. Les thermistances remplissent différentes tâches, par ex. compensation de température ou détection de température dans un circuit de protection contre la surchauffe. ([https://www.tdk-electronics.tdk.com/download/531136/5608e4b12153bb12af2808fbedc5a55b/pdf-applicationnotes.pdf note d’application])
 
  
−
==Pont diviseur==
+
'''Exemple : ''' [https://www.tdk-electronics.tdk.com/download/531136/5608e4b12153bb12af2808fbedc5a55b/pdf-applicationnotes.pdf note d’application]
  
−
On place la CTN dans un pont diviseur (cf figure ci dessous).
 
  
−
#Lorsque la température change :
+
==Utilisation : avec un pont diviseur==
−
#la valeur de la CTN change
+
 
−
#donc la tension Vθ change
+
On place la {{Rouge|CTN}} dans un {{Rouge|pont diviseur}} (cf figure ci dessous).
−
#on mesure cette tension qui permet d'en déduire la valeur de la température.
+
 
 +
Lorsque la {{Rouge|température change}} :
 +
*la {{Rouge|valeur}} (résistance) de la {{Rouge|CTN}} change
 +
*donc la tension {{Rouge|Vθ change}}
 +
*la {{Rouge|mesure cette tension}} permet d'en {{Rouge|déduire}} la valeur de la {{Rouge|température}}.
  
 
{|
 
{|
Ligne 60 : Ligne 63 :
  
  
−
===Etape 1 : relation V<sub>θ</sub>=f(R<sub>θ</sub>) ===
+
==Analyse==
−
{{Question|Exprimez la relation entre}}
 
  
−
V<sub>θ</sub> = f(Vcc, R1 et Rθ)
+
{{Rouge|'''Travail de groupe''' avec 1 étudiant à tour de rôle au tableau sur chaque point}}
  
−
'''Remarque''' :
 
−
*θ est la température, exprimée en Kelvin
 
  
−
===Etape 2 : caractéristique résistance / température ===
 
  
−
On considère que sur une plage de température, la résistance de la thermistance est :
+
Nous allons exprimer les différentes relations et compléter progressivement une feuille de calcul sur un tableur.
  
−
[[Fichier:EquationRteta.png|300px]]
+
*'''Créer''' une feuille de calcul ( par ex : https://docs.google.com/spreadsheets/create?hl=fr )
 +
**mettre une colonne température exprimée en °C (de -30° à 100°C par ex)
 +
**ajouter une 2nde colonne en y calculant la température exprimée en K
 +
*on peut alors '''calculer''' la valeur de Rθ en fonction de la température dans une 3ème colonne
 +
** [[Fichier:EquationRteta.png|200px]]
 +
**R<sub>25°C</sub> = 8200Ω, β = 3480 K, T<sub>25°C</sub> = 273+25 , avec θ en K
 +
**on vérifiera que la résistance à 25°C est bien 8200Ω (valeur de R<sub>25°C</sub> )
 +
**le tracé de la courbe (Rθ en fonction de θ ) permet de vérifier qu'il s'agit bien d'une CTN
  
−
avec R<sub>25°C</sub> = 8200Ω, β = 3480 K, T<sub>25°C</sub> = 273+25
+
*'''ajout''' de Vθ
−
et θ exprimée en Kelvin
+
**exprimer la valeur de Vθ en fonction de Rθ
 +
**on trouvera la valeur de R1 sur le schéma de la carte
 +
**ajouter une colonne avec Vθ sur votre feuille de calcul
  
−
Exemple : pour θ = 50°C
+
*'''mesure''' de Vθ à l'aide du CAN
−
 
+
**[[Fichier:symbolCAN.png|300px]]<br>https://fr.wikipedia.org/wiki/Convertisseur_analogique-num%C3%A9rique
−
[[Fichier:EquationRteta50.png|400px]]
+
**un CAN convertit '''linéairement''' une tension (pour nous entre 0 et 5V ) en un nombre ( pour nous entre 0 et 1023)
−
 
+
**on repère les broches utilisables pour le CAN sur les cartes arduino par le préfixe A : A0|A1|A2 ...
−
 
+
**ajouter la colonne donnant la valeur du CAN en fonction de Vθ
−
{{Question|  En utilisant la feuille de calculs suivante, déterminez la résistance de la CTN sur la plage de température. On rappelle que la fonction exponentielle est EXP.}}
+
**de façon général N=V<sub>θ</sub>/q avec q=Vref/(2<sup>n</sup>-1) le quantum et n la résolution du CAN (8 ou 10 bits)
−
 
 
−
[https://docs.google.com/spreadsheets/d/1ghO5RSVVjw-UM_H2PW3N0rkWTHNPdlSzlwZ7YM-V1K8/edit?usp=sharing lien vers la feuille]
 
−
 
 
−
 
 
−
{{Question|La résistance R1 (12 k), en utilisant la feuille de calculs du fichier, déterminez :}}
 
−
la tension V<sub>θ</sub> sur la plage de température avec Vcc = 5 V
 
−
 
 
−
 
 
−
===Etape 3 : Conversion de la tension en nombre numérique puis en température===
 
−
 
 
−
[[Fichier:symbolCAN.png|300px]]
 
−
 
 
−
'''Principe de fonctionnement du CAN'''
 
−
 
 
−
On entre une tension analogique V<sub>θ</sub> et on ressort un nombre numérique en binaire sous n fils suivant la résolution du CAN.
 
−
 
 
−
Exemple pour la carte NANO
 
−
*La résolution n peut être de 10 bits ou de 8 bits soit 1024 ou 256 combinaisons.
 
−
*La tension de référence Vréf est soit de 5V soit de 1,1V
 
−
 
 
−
Pour Vréf = 5V :
 
−
 
 
−
[[Fichier:TableauCAN.png|600px]]
 
−
 
 
−
La tension de '''0,0196 V''' est appelée le quantum. On a une résolution de '''20 mV'''
 
−
 
 
−
[[Fichier:caracteristiqueCAN.png|600px]]
 
−
 
 
−
Quand la tension analogique Vθ varie linéairement de 0 à Vréf la valeur numérique évolue en palier de 0 à 255 en pas d’un quantum soit environ 20 mV. Le quantum est aussi appelé le LSB le bit le moins significatif (Least Significant Bit).
 
−
 
 
−
Pour n = 10 bits
 
−
 
 
−
[[Fichier:TableauCAN_10bits.png|600px]]
 
−
 
 
−
En utilisant n = 10 bits la résolution est meilleure car le quantum est de 5 mV mais le temps de conversion est plus long.
 
−
Pour la tension de référence de 1,1V on remplace simplement la colonne Volt de 0 à 1,1 V, au-delà de 1,1 V jusqu’à 5V, le convertisseur est saturé, la valeur numérique reste constante à 255 ou 1023 suivant la résolution 8 ou 10 bits. Le quantum sera respectivement de 4,3 mV et 1 mV environ.
 
−
 
 
−
{{Question|Déterminer la valeur de la résistance R1 pour la plage de température afin que la tension V ne dépasse pas la tension de référence de 1,1 V.}}
 
−
 
 
−
'''Maintenant déterminons la température en fonction de la valeur numérique du convertisseur'''
 
−
 
 
−
Dans le premier saé nous avions affiché l’image de la température en volt. Maintenant nous somme en mesure après quelques petits calculs d’afficher la température en degré Celsius.
 
−
 
 
−
{{Question|Exprimez la température θ en utilisant la formule :}}
 
−
 
 
−
[[Fichier:EquationRteta.png|300px]]
 
−
 
 
−
Pour déterminer la température θ il nous faut R<sub>θ</sub> qui est l’inconnu dans l’équation.
 
−
 
 
−
{{Question|Exprimez : }}la résistance Rθ en utilisant la formule Vθ = f(Vcc, R1 et Rθ).trouvée à la première question.
 
−
 
 
−
Sachant que la valeur numérique N=V<sub>θ</sub>/q avec q=Vref/(2<sup>n</sup>-1) le quantum et n la résolution du CAN (8 ou 10 bits)
 
−
 
 
−
{{Question|Exprimez la formule de la température en degré Celsius en fonction de la valeur N du convertisseur analogique.}}
 
  
 
=Programmation=
 
=Programmation=
Ligne 173 : Ligne 127 :
 
*ajouter un peu de texte, [https://www.arduino.cc/reference/en/language/functions/communication/serial/print/ cf Serial.print()] (ou Serial.println() pour un retour à la ligne après le message)
 
*ajouter un peu de texte, [https://www.arduino.cc/reference/en/language/functions/communication/serial/print/ cf Serial.print()] (ou Serial.println() pour un retour à la ligne après le message)
  
−
==calculer la valeur de la tension==
+
==Remontons à la température==
−
 
 
−
Nous avons trouvé la relation entre la valeur du CAN et la tension aux bornes de la CTN.
 
−
 
 
−
{{Question|Afficher en plus de la valeur du CAN la tension correspondante.}}
 
  
−
==calcul Rteta==
+
On reprend alors les calculs en inversant les équations et en affichant les valeurs succseives sur la liaison série :
 +
*calculer et afficher Vθ sur la liaison série
 +
*on peut ensuite calculer la valeur de Rθ
 +
*puis la valeur de la température en K
 +
*et enfin la valeur de la température en °C
  
−
==calcul teta==
+
=plage de température=
  
−
=affichage sur leds couleur=
+
on souhaite avoir une indication visuelle de la température à l'aide des 2 leds :
 +
*si T<0°C, on allume la led de gauche
 +
*si 0°C<T<10°C on allume la led de droite
 +
*si T>10°C on allume les 2 leds

Version actuelle datée du 3 juillet 2024 à 14:22

Mesure de température par CTN

Principe

La mesure d'une grandeur physique (température, pression, vitesse ...) nécessite l'utilisation d'un capteur. Il s'agit d'un composant dont le comportement varie en fonction de la valeur mesurée.


Parmi les capteurs de température, nous allons nous intéresser aux thermistances :

  • le préfixe thermi indique qu'il est sensible à la température
  • le suffixe stance indique qu'il s'agit d'une résistance
Une thermistance est un capteur dont la valeur de résistance dépend de la température

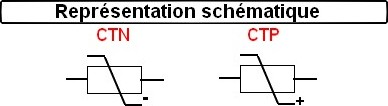
On distingue les thermistances :

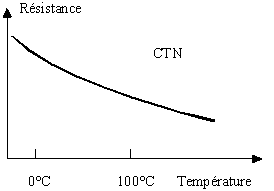
  • CTN : la valeur de la résistance diminue lorsque la température augmente
  • CTP : la valeur de la résistance augmente lorsque la température augmente
Symbole du composant Valeur de la résistance en fct de la température pour une CTN
SymbolesCTNCTP.png CaracteristiqueCTN.png 


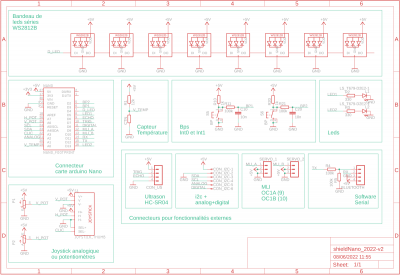
Sur le shield arduino, nous utilisons une CTN


On constate sur la courbe précédente que la valeur de la CTN n'est pas linéaire en fonction de la température. 

la mesure de température ou la compensation dans une grande variété d'applications.


Usage : Les thermistances sont utilisées pour

  • la mesure de température
  • détection de surchauffe
  • la compensation en température ( compensation de la variation de la caractéristique de composants lorsque la température change)


Exemple : note d’application


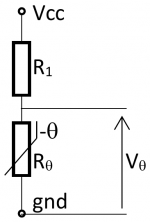
Utilisation : avec un pont diviseur

On place la CTN dans un pont diviseur (cf figure ci dessous).

Lorsque la température change :

  • la valeur (résistance) de la CTN change
  • donc la tension Vθ change
  • la mesure cette tension permet d'en déduire la valeur de la température.
DiviseurCTN.png
  • R1 résistance fixe
  • Rθ résistance variable en fonction de la température
  • Vθ tension image de la température
  • Vcc tension d’alimentation du montage
  • gnd tension de référence (masse 0V)


Analyse

Travail de groupe avec 1 étudiant à tour de rôle au tableau sur chaque point


Nous allons exprimer les différentes relations et compléter progressivement une feuille de calcul sur un tableur.

  • Créer une feuille de calcul ( par ex : https://docs.google.com/spreadsheets/create?hl=fr )
    • mettre une colonne température exprimée en °C (de -30° à 100°C par ex)
    • ajouter une 2nde colonne en y calculant la température exprimée en K
  • on peut alors calculer la valeur de Rθ en fonction de la température dans une 3ème colonne
    • EquationRteta.png
    • R25°C = 8200Ω, β = 3480 K, T25°C = 273+25 , avec θ en K
    • on vérifiera que la résistance à 25°C est bien 8200Ω (valeur de R25°C )
    • le tracé de la courbe (Rθ en fonction de θ ) permet de vérifier qu'il s'agit bien d'une CTN
  • ajout de Vθ
    • exprimer la valeur de Vθ en fonction de Rθ
    • on trouvera la valeur de R1 sur le schéma de la carte
    • ajouter une colonne avec Vθ sur votre feuille de calcul
  • mesure de Vθ à l'aide du CAN
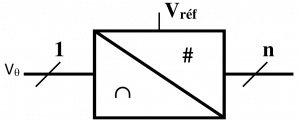
    • SymbolCAN.png
      https://fr.wikipedia.org/wiki/Convertisseur_analogique-num%C3%A9rique
    • un CAN convertit linéairement une tension (pour nous entre 0 et 5V ) en un nombre ( pour nous entre 0 et 1023)
    • on repère les broches utilisables pour le CAN sur les cartes arduino par le préfixe A : A0|A1|A2 ...
    • ajouter la colonne donnant la valeur du CAN en fonction de Vθ
    • de façon général N=Vθ/q avec q=Vref/(2n-1) le quantum et n la résolution du CAN (8 ou 10 bits)

Programmation

SchemaShieldNano.png

Nous avons exploré dans les Tps précédents les e/s binaires. Ici nous nous intéresserons aux entrées analogiques et utiliserons la fonction analogRead() permettant de lire l'état d'une des entrées analogiques.

Vous utiliserez la liaison série afin de vérifier le bon fonctionnement de votre programme


afficher la valeur du can sur liaison série

L'exemple suivant permet de lire la valeur du Convertisseur Analogique Numérique (CAN) sur la broche A2. 

// the setup routine runs once when you press reset:
void setup()
{
  // initialize serial communication at 9600 bits per second:
  Serial.begin(9600);
}
// the loop routine runs over and over again forever:
void loop()
{
  // read the input on analog pin 2:
  int sensorValue = analogRead(A2);
  // print out the value you read:
  Serial.println(sensorValue);
}

Question.jpg Modifier le programme pour afficher la valeur sur la broche qui nous intéresse !

Remarque :

  • ça peut être intéressant de ralentir un peu tout ça !
  • ajouter un peu de texte, cf Serial.print() (ou Serial.println() pour un retour à la ligne après le message)

Remontons à la température

On reprend alors les calculs en inversant les équations et en affichant les valeurs succseives sur la liaison série :

  • calculer et afficher Vθ sur la liaison série
  • on peut ensuite calculer la valeur de Rθ
  • puis la valeur de la température en K
  • et enfin la valeur de la température en °C

plage de température

on souhaite avoir une indication visuelle de la température à l'aide des 2 leds :

  • si T<0°C, on allume la led de gauche
  • si 0°C<T<10°C on allume la led de droite
  • si T>10°C on allume les 2 leds
Récupérée de « http://wikigeii.iut-troyes.univ-reims.fr//index.php?title=Cours:ArduinoTemperature&oldid=19036 »